Investigations into Multicolor Peg Solitaire
The game of peg solitaire has a rich and complex history. Many are familiar with the game and its seemingly simple rules: “jump” a peg and it disappears, and repeat until there is one peg remaining. However, a deeper analysis of peg solitaire reveals rich mathematical ideas behind both the strategy and solvability of the game. Boards can come in many different shapes; the most prominent of which have been listed below:
On the first 5 board layouts, moves are made by jumping pegs either horizontally or vertically. The 6th board, however, allows jumps in 6 different directions: one for each side of the hexagons. The solvability of these boards is well-established; however, less work has been done on different variations of the game. Our research focused specifically on peg solitaire in 3 colors on a triangle graph.
Analysis on traditional peg solitaire on triangle boards (board 6) can be found in the work of George Bell, who published a paper in 2008 titled “Solving Triangular Peg Solitaire.” My advisor and I extend this work to a variation on the traditional rules where the concept of “colors” is introduced to the graph. The normal game of peg solitaire can be conceptualized as having two colors: one for an empty hole and one for a peg. We added a third color to the game, representing a different color of peg. Under this new ruleset, if a peg is jumped over a peg of the same color, the peg that was jumped over switches to be the other color. If a peg is jumped over a peg of a differing color, the jumped peg is removed as normal:
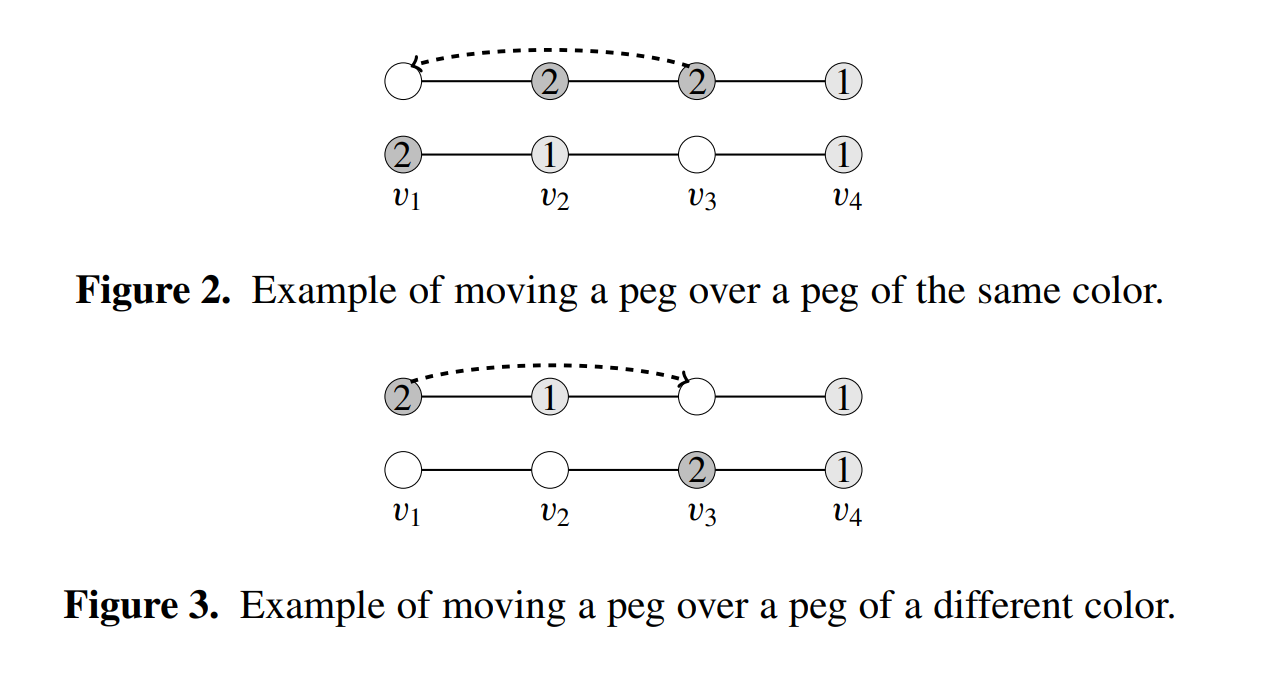
Adding this ruleset drastically changes what we know about the solvability of different types of graphs. Until recently, this section was titled “Investigations into 3-color Peg Solitaire,” but recently we expanded our focus to all numbers of colors through a generalization of the ruleset.
Under the guidance of my advisor, Dr. Lauren Grimley, I have done work to prove the solvability of all triangle boards for all colors, and have inductively proven the number of starting positions on triangle boards up to symmetry.
Our work is currently quite volatile, as new solution strategies are uncovered quite frequently. For the most current information available, feel free to email me.